Презентация на тему: Квантовая физика

Квантовая физика Лекция 16

Тепловое излучение тел Испускаемый источником свет уносит с собой энергию. Существует много различных механизмов подвода энергии к источнику света. В тех случаях, когда необходимая энергия сообщается нагреванием, т. е. подводом тепла, излучение называется тепловым или температурным. В состоянии равновесия процессы испускания и поглощения энергии каждым телом в среднем компенсируют друг друга, и в пространстве между телами плотность энергии излучения достигает определенного значения, зависящего только от установившейся температуры тел. Это излучение, находящееся в термодинамическом равновесии с телами, имеющими определенную температуру, называется равновесным или черным излучением.

Распределение энергии по длинам волн в излучении абсолютно черного тела при заданной температуре T характеризуется излучательной способностью r(λ, T), равной мощности излучения с единицы поверхности тела в единичном интервале длин волн. Произведение r(λ, T)Δλ равно мощности излучения, испускаемого единичной площадкой поверхности по всем направлениям в интервале Δλ длин волн. Аналогично можно ввести распределение энергии по частотам r(ν, T). Функцию r(λ, T) (или r(ν, T)) часто называют спектральной светимостью, а полный поток R(T) излучения всех длин волн, равный Распределение энергии по длинам волн в излучении абсолютно черного тела при заданной температуре T характеризуется излучательной способностью r(λ, T), равной мощности излучения с единицы поверхности тела в единичном интервале длин волн. Произведение r(λ, T)Δλ равно мощности излучения, испускаемого единичной площадкой поверхности по всем направлениям в интервале Δλ длин волн. Аналогично можно ввести распределение энергии по частотам r(ν, T). Функцию r(λ, T) (или r(ν, T)) часто называют спектральной светимостью, а полный поток R(T) излучения всех длин волн, равный называют интегральной светимостью тела.

В 1879 году Йозеф Стефан на основе анализа экспериментальных данных пришел к заключению, что интегральная светимость R(T) абсолютно черного тела пропорциональна четвертой степени абсолютной температуры T: В 1879 году Йозеф Стефан на основе анализа экспериментальных данных пришел к заключению, что интегральная светимость R(T) абсолютно черного тела пропорциональна четвертой степени абсолютной температуры T: R(T) = σT4. Этот закон получил название закона Стефана–Больцмана. Числовое значение постоянной σ, по современным измерениям, составляет σ = 5,671·10–8 Вт / (м2 · К4).

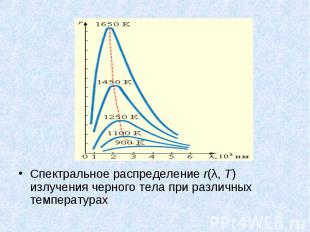
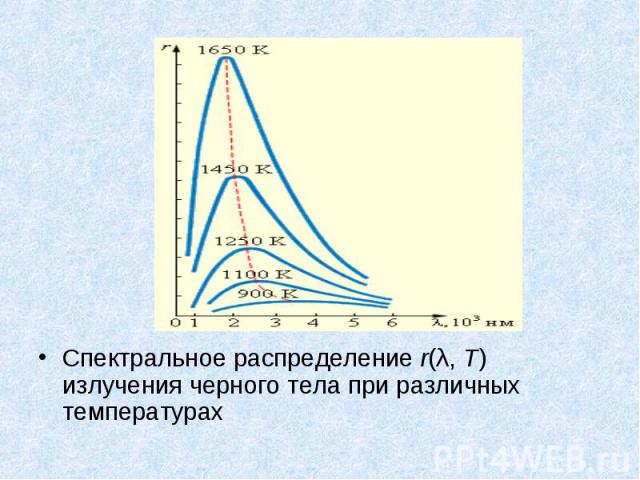
Спектральное распределение r(λ, T) излучения черного тела при различных температурах Спектральное распределение r(λ, T) излучения черного тела при различных температурах

С увеличением температуры максимум смещается в область коротких длин волн, причем произведение температуры T на длину волны λm, соответствующую максимуму, остается постоянным: λmT = b   или   λm = b / T. С увеличением температуры максимум смещается в область коротких длин волн, причем произведение температуры T на длину волны λm, соответствующую максимуму, остается постоянным: λmT = b   или   λm = b / T. Это соотношение ранее было получено Вином из термодинамики. Оно выражает так называемый закон смещения Вина: длина волны λm, на которую приходится максимум энергии излучения абсолютно черного тела, обратно пропорциональна абсолютной температуре T. Значение постоянной Вина b = 2,898·10–3 м·К.

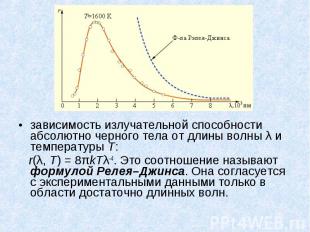
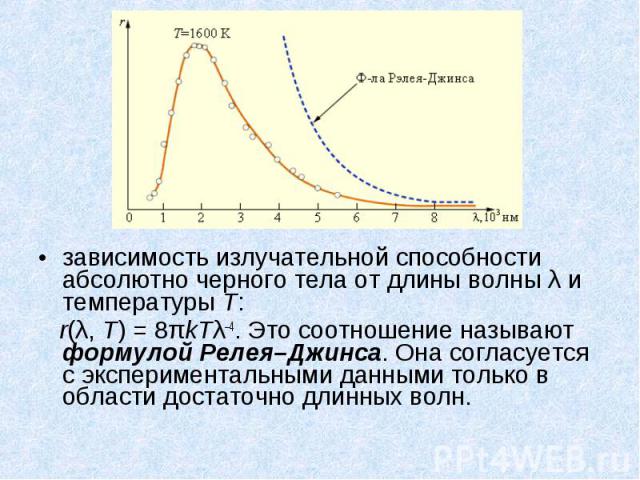
зависимость излучательной способности абсолютно черного тела от длины волны λ и температуры T: зависимость излучательной способности абсолютно черного тела от длины волны λ и температуры T: r(λ, T) = 8πkTλ–4. Это соотношение называют формулой Релея–Джинса. Она согласуется с экспериментальными данными только в области достаточно длинных волн.

Процессы излучения и поглощения нагретым телом электромагнитной энергии, происходят не непрерывно, как это принимала классическая физика, а конечными порциями – квантами. Квант – это минимальная порция энергии, излучаемой или поглощаемой телом. По теории Планка, энергия кванта E прямо пропорциональна частоте света: Процессы излучения и поглощения нагретым телом электромагнитной энергии, происходят не непрерывно, как это принимала классическая физика, а конечными порциями – квантами. Квант – это минимальная порция энергии, излучаемой или поглощаемой телом. По теории Планка, энергия кванта E прямо пропорциональна частоте света: E = hν, где h – так называемая постоянная Планка, равная h = 6,626·10–34 Дж·с. Постоянная Планка – это универсальная константа, которая в квантовой физике играет ту же роль, что и скорость света в СТО.

Фотоэффект. Фотоны Фотоэлектрический эффект был открыт в 1887 году немецким физиком Г. Герцем и в 1888–1890 годах экспериментально исследован А. Г. Столетовым. Наиболее полное исследование явления фотоэффекта было выполнено Ф. Леонардом в 1900 г. К этому времени уже был открыт электрон (Д. Томсон, 1897 г.), и стало ясно, что фотоэффект (или точнее – внешний фотоэффект) состоит в вырывании электронов из вещества под действием падающего на него света.

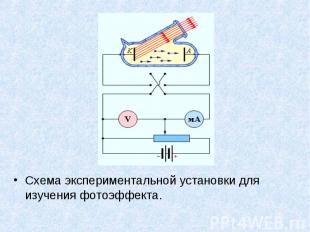
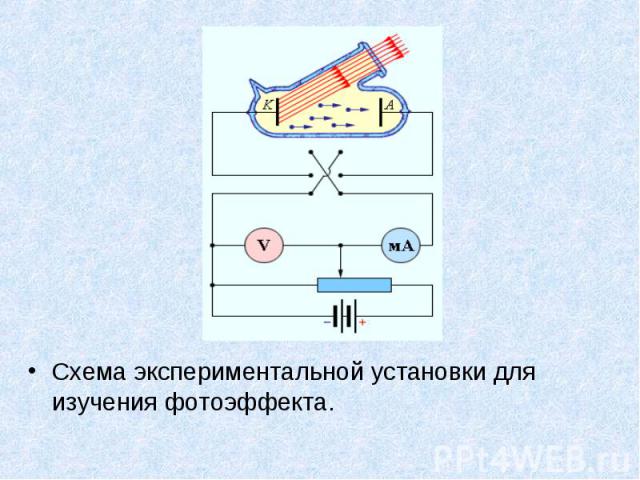
Схема экспериментальной установки для изучения фотоэффекта. Схема экспериментальной установки для изучения фотоэффекта.

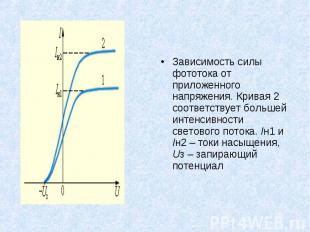
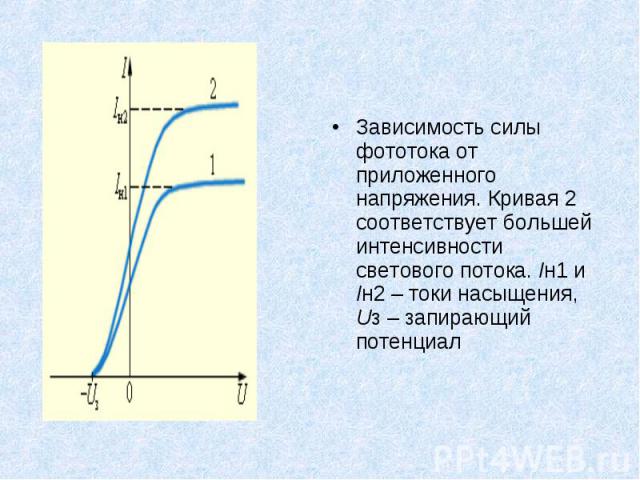
Зависимость силы фототока от приложенного напряжения. Кривая 2 соответствует большей интенсивности светового потока. Iн1 и Iн2 – токи насыщения, Uз – запирающий потенциал Зависимость силы фототока от приложенного напряжения. Кривая 2 соответствует большей интенсивности светового потока. Iн1 и Iн2 – токи насыщения, Uз – запирающий потенциал

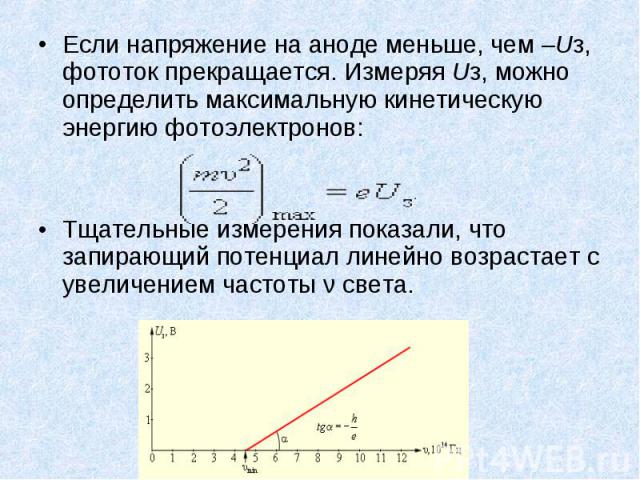
Если напряжение на аноде меньше, чем –Uз, фототок прекращается. Измеряя Uз, можно определить максимальную кинетическую энергию фотоэлектронов: Если напряжение на аноде меньше, чем –Uз, фототок прекращается. Измеряя Uз, можно определить максимальную кинетическую энергию фотоэлектронов: Тщательные измерения показали, что запирающий потенциал линейно возрастает с увеличением частоты ν света.

Многочисленными экспериментаторами были установлены следующие основные закономерности фотоэффекта: Многочисленными экспериментаторами были установлены следующие основные закономерности фотоэффекта: Максимальная кинетическая энергия фотоэлектронов линейно возрастает с увеличением частоты света ν и не зависит от его интенсивности. Для каждого вещества существует так называемая красная граница фотоэффекта, т. е. наименьшая частота νmin, при которой еще возможен внешний фотоэффект. Число фотоэлектронов, вырываемых светом из катода за 1 с, прямо пропорционально интенсивности света. Фотоэффект практически безынерционен, фототок возникает мгновенно после начала освещения катода при условии, что частота света ν > νmin.

Свет имеет прерывистую дискретную структуру. Электромагнитная волна состоит из отдельных порций – квантов, впоследствии названных фотонами. При взаимодействии с веществом фотон целиком передает всю свою энергию hν одному электрону. Часть этой энергии электрон может рассеять при столкновениях с атомами вещества. Кроме того, часть энергии электрона затрачивается на преодоление потенциального барьера на границе металл–вакуум. Для этого электрон должен совершить работу выхода A, зависящую от свойств материала катода. Наибольшая кинетическая энергия, которую может иметь вылетевший из катода фотоэлектрон, определяется законом сохранения энергии: Свет имеет прерывистую дискретную структуру. Электромагнитная волна состоит из отдельных порций – квантов, впоследствии названных фотонами. При взаимодействии с веществом фотон целиком передает всю свою энергию hν одному электрону. Часть этой энергии электрон может рассеять при столкновениях с атомами вещества. Кроме того, часть энергии электрона затрачивается на преодоление потенциального барьера на границе металл–вакуум. Для этого электрон должен совершить работу выхода A, зависящую от свойств материала катода. Наибольшая кинетическая энергия, которую может иметь вылетевший из катода фотоэлектрон, определяется законом сохранения энергии: Эту формулу принято называть уравнением Эйнштейна для фотоэффекта.

Фотон движется в вакууме со скоростью c. Фотон не имеет массы, m = 0. Из общего соотношения специальной теории относительности, связывающего энергию, импульс и массу любой частицы, Фотон движется в вакууме со скоростью c. Фотон не имеет массы, m = 0. Из общего соотношения специальной теории относительности, связывающего энергию, импульс и массу любой частицы, E2 = m2c4 + p2c2, следует, что фотон обладает импульсом

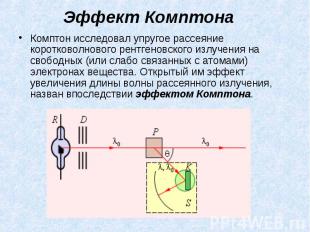
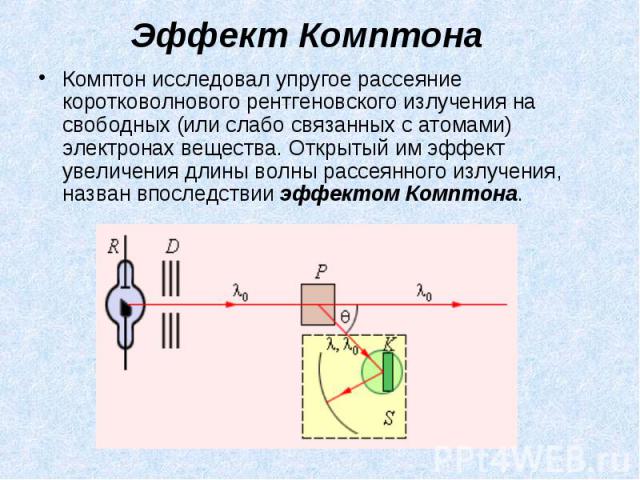
Эффект Комптона Комптон исследовал упругое рассеяние коротковолнового рентгеновского излучения на свободных (или слабо связанных с атомами) электронах вещества. Открытый им эффект увеличения длины волны рассеянного излучения, назван впоследствии эффектом Комптона.

Опыт показал, что в рассеянном излучении наблюдается увеличение длины волны Δλ, зависящее от угла рассеяния θ: Опыт показал, что в рассеянном излучении наблюдается увеличение длины волны Δλ, зависящее от угла рассеяния θ: Δλ = λ - λ0 = 2Λ sin2 θ / 2, где Λ = 2,43·10–3 нм – так называемая комптоновская длина волны, не зависящая от свойств рассеивающего вещества. В рассеянном излучении наряду со спектральной линией с длиной волны λ наблюдается несмещенная линия с длиной волны λ0.

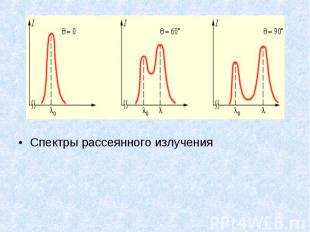
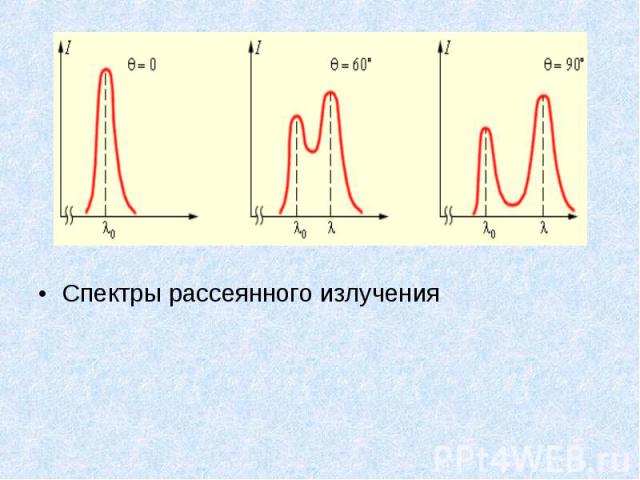
Спектры рассеянного излучения Спектры рассеянного излучения

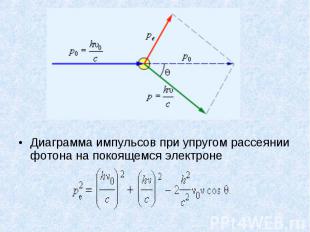
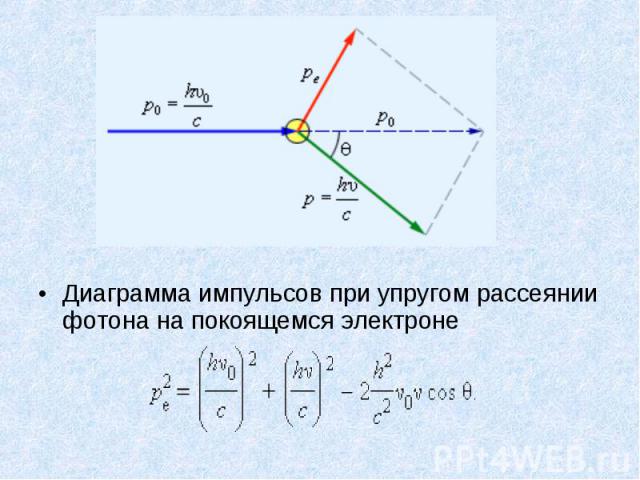
Диаграмма импульсов при упругом рассеянии фотона на покоящемся электроне Диаграмма импульсов при упругом рассеянии фотона на покоящемся электроне

Теоретический расчет, выполненный на основе квантовых представлений, дал исчерпывающее объяснение эффекту Комптона и позволил выразить комптоновскую длину волны Λ через фундаментальные константы h, c и m: Теоретический расчет, выполненный на основе квантовых представлений, дал исчерпывающее объяснение эффекту Комптона и позволил выразить комптоновскую длину волны Λ через фундаментальные константы h, c и m:

Волновые свойства микрочастиц. Дифракция электронов С каждым микрообъектом связаны, с одной стороны, корпускулярные характеристики – энергия E и импульс p, а с другой стороны, волновые характеристики – частота ν и длина волны λ. Корпускулярные и волновые характеристики микрообъектов связаны такими же количественными соотношениями, как и у фотона:

Гипотеза де Бройля постулировала эти соотношения для всех микрочастиц, в том числе и для таких, которые обладают массой m. Любой частице, обладающей импульсом, сопоставлялся волновой процесс с длиной волны λ = h / p. Для частиц, имеющих массу, Гипотеза де Бройля постулировала эти соотношения для всех микрочастиц, в том числе и для таких, которые обладают массой m. Любой частице, обладающей импульсом, сопоставлялся волновой процесс с длиной волны λ = h / p. Для частиц, имеющих массу,

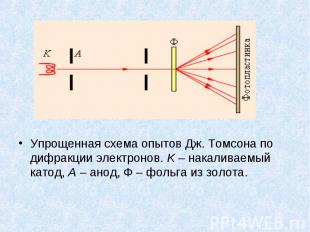
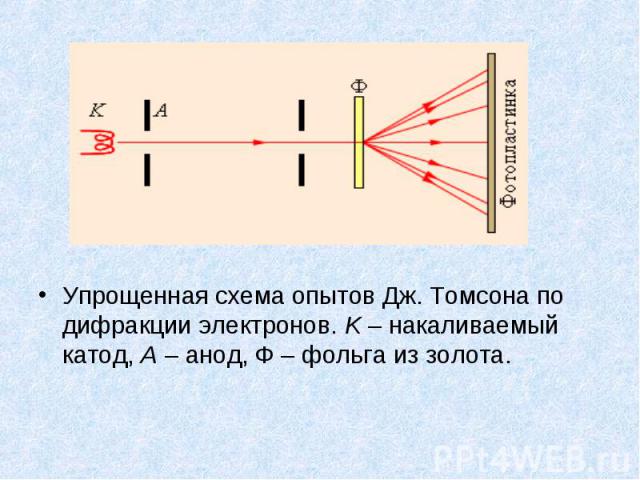
Упрощенная схема опытов Дж. Томсона по дифракции электронов. K – накаливаемый катод, A – анод, Ф – фольга из золота. Упрощенная схема опытов Дж. Томсона по дифракции электронов. K – накаливаемый катод, A – анод, Ф – фольга из золота.

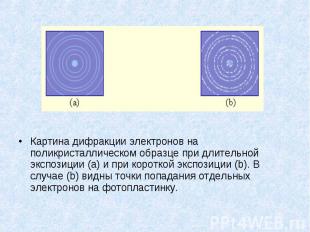
Картина дифракции электронов на поликристаллическом образце при длительной экспозиции (a) и при короткой экспозиции (b). В случае (b) видны точки попадания отдельных электронов на фотопластинку. Картина дифракции электронов на поликристаллическом образце при длительной экспозиции (a) и при короткой экспозиции (b). В случае (b) видны точки попадания отдельных электронов на фотопластинку.

Таким образом, было экспериментально доказано, что волновые свойства присущи не только большой совокупности электронов, но и каждому электрону в отдельности. Таким образом, было экспериментально доказано, что волновые свойства присущи не только большой совокупности электронов, но и каждому электрону в отдельности. Впоследствии дифракционные явления были обнаружены также для нейтронов, протонов, атомных и молекулярных пучков. Экспериментальное доказательство наличия волновых свойств микрочастиц привело к выводу о том, что это универсальное явление природы, общее свойство материи. Следовательно, волновые свойства должны быть присущи и макроскопическим телам. В квантовой механике для характеристики состояний объектов в микромире вводится понятие волновой функции Ψ (пси-функции). Квадрат модуля волновой функции |Ψ|2 пропорционален вероятности нахождения микрочастицы в единичном объеме пространства. Конкретный вид волновой функции определяется внешними условиями, в которых находится микрочастица. . Математический аппарат квантовой механики позволяет находить волновую функцию частицы, находящейся в заданных силовых полях. Безграничная монохроматическая волна де Бройля есть волновая функция свободной частицы, на которую не действуют никакие силовые поля.