Презентация на тему: Конвективный теплообмен

Тема13. Конвективный теплообмен. Условия подобия процессов конвективного теплообмена. Критериальные уравнения. 13.1 ТЕПЛООТДАЧА ПРИ ЛАМИНАРНОМ ТЕЧЕНИИ ЖИДКОСТИ В ТРУБАХ. При ламинарном течении наряду с поперечным переносом тепла путем теплопроводности происходит также конвективный перенос тепла в продольном направлении. Вследствие этого теплообмен при ламинарном режиме течения зависит от гидродинамической картины течения.Пусть во входном сечении tж=const и отличается от tc. По мере движения потока между жидкостью и стенкой происходит процесс теплообмена и tж постепенно изменяется. Таким образом, развитие процесса теплообмена внутри труб, вначале качественно такое же, как и в ламинарном погранслое на пластине. Около поврхности трубы образуется тепловой погранслой, толщина которого постепенно увеличивается в направлении движения потока. На некотором расстоянии от входа трубы lн.т тепловые погран слои смыкаются, и в процессе теплообмена учавствует далее весь поток жидкости. Расстояние lн.т. можно приближенно оценить по зависимости . Обычно на практике ламинарный режим встречается при течении вязких тепло носителей, таких, как различные масла, для которых значение Pr 1. В таких случаях длинна участка тепловой стабилизации lн.т. оказывается довольно большой. Так например, если Re=200 и Pr=500? то lн.т 5 .

На расстоянии большем, чем lн.т. профиль температур по сечению трубы продолжает изменяться, как это показано на рис 13.1 На расстоянии большем, чем lн.т. профиль температур по сечению трубы продолжает изменяться, как это показано на рис 13.1 Рис.13.1. Изменение распределения температур по сечению и длине тубы. В пределах участка тепловой стабилизации температурный градиент в жидкости у стенки убывает по мере увеличения расстояния от входа быстрее, чем температурный напор , так как центральная часть потока еще не участвует в теплообмене. Поэтому из дифференциального уравнения теплообмена 13.1 Следует, что локальный коэффициент теплоотдачи постепенно уменьшается вдоль трубы. Падение продолжается до тех пор, пока тепловые погранслои не смыкаются. Далее обе величины и убывают с одинаковой скоростью, а

На рис 13.2. показано изменение и от длины трубы. Этот график показывает, что расстояние, на котором происходит стабилизация всегда больше расстояния, отвечающего стабилизации локальных коэффициентов теплоотдачи,- . На рис 13.2. показано изменение и от длины трубы. Этот график показывает, что расстояние, на котором происходит стабилизация всегда больше расстояния, отвечающего стабилизации локальных коэффициентов теплоотдачи,- . В уравнении (13.1) величина есть средняя температура потока в данном сечении. Эту температуру называют также температурой смещения. Температура определяется из выражения: 13.2 Если зависимостью Cp и от температуры можно пренебречь, то (13.2) принимает вид: 13.2.а В первом случае (13.2) осреднение температуры производится по энтальпии жидкости, во втором (13.2.а) – по ее объемному расходу. Следовательно, чтобы произвести осреднение температуры в сечении, необходимо иметь

Распределение скорости и температуры, измеренной одновременно (Рис 13.3). Если же скорость по сечению канала одинакова, то формула осреднения примет вид: Распределение скорости и температуры, измеренной одновременно (Рис 13.3). Если же скорость по сечению канала одинакова, то формула осреднения примет вид: 13.2.б Величина (13.1) представляет собой локальную плоскость теплового потока в данном сечении. Для расчета среднего коэффициента теплоотдачи 13.3 Необходимо в общем случае знать средне по длине трубы или канала . Если температура изменяется не значительно, то осреднение температуры по длине производится следующим образом: Рис.13.2 Изменение локального и Рис.13.3 Изменение скорости среднего коэффициентов теплоотдачи и температуры по сечению от длинны трубы.

При небольшом изменении температуры вдоль трубы величина определяется как среднеарифметическое из температур в начальном и конечном сечении тубы: При небольшом изменении температуры вдоль трубы величина определяется как среднеарифметическое из температур в начальном и конечном сечении тубы: 14.5 На практике обычно скорость и температура на выходе в трубу имею т профили, близкие к равномерным. Для этих условий расчет среднего коэффициента теплоотдачи при ламинарном режиме течения жидкости в тубах при l/d>10 и >10 проводится по формуле 13.5 Соотношение (13.5) справедливо для значений 0,06< Соотношение (13.5) правомерно при значениях: При меньших значениях этой величины, т.е. для труб весьма большой длины: l/d>0.067 (13.6) величина становится постоянной , что отвечает условиям стабилизации интенсивности теплопередачи. При выполнении этих условий вместо (13.5) для определения среднего коэффициента теплоотдачи может быть рекомендовано приближенное соотношение: (13.7)

13.2. ТЕПЛООТДАЧА ПРИ ТУРБУЛЕНТНОМ РЕЖИМЕ. 13.2. ТЕПЛООТДАЧА ПРИ ТУРБУЛЕНТНОМ РЕЖИМЕ. При турбулентном режиме движения перенос тепла внутри жидкости осуществляется в основном путем перемешивания. При этом процесс перемешивания протекает настолько эффективно, что по сечению ядра потока температура жидкости практически постоянна. Резкое изменение температуры наблюдается лишь внутри тонкого слоя у поверхности. Было проведено большое количество исследований с различными каналами и разного рода жидкостями в широком диапазоне изменения основных параметров. На основе анализа и обобщения результатов этих исследований для расчета средней теплоотдачи установлена зависимость (13.8) За определяющую температуру здесь принята средняя температура жидкости , а за определяющий размер – эквивалентный диаметр dэк: Dэк= ut/u, где t – площадь поперечного сечения канала; u – полный периметр канала. Коэффициент El учитывает изменение среднего коэффициента теплоотдачи по длине трубы. Если l/d>50, то El=1. При l/d<50 необходимо учитывать влияние начального термического участка.

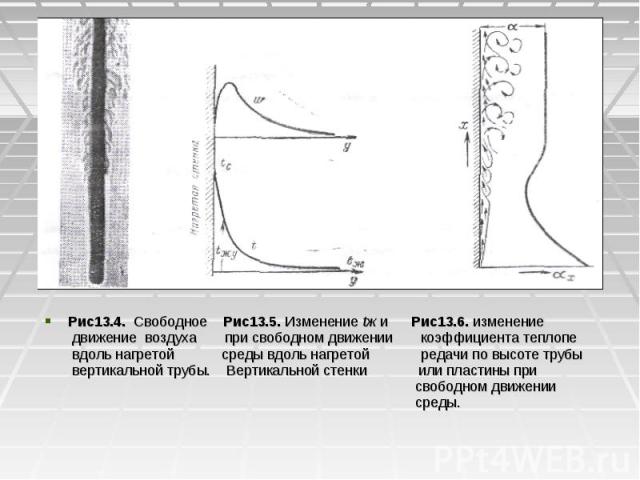
13.3 ТЕПЛООТДАЧА ПРИ ЕСТЕСТВЕННОЙ КОНВЕКЦИИ. 13.3.1. Теплопередача в неограниченном пространстве. Процесс теплообмена при естественной конвекции (свободное движение) имеет очень широкое распространение как в технике, так ив быту. Свободным называется движение жидкости вследствие разности плотностей нагретых и холодных частиц. На Рис13.4 показана типичная картина движения нагретого воздуха вдоль вертикальной трубы. При свободном движении жидкости в пограничном слое темпе-ратура жидкости изменяется от tc до tж а скорость —от нуля у стенки, проходит через максимум и на большом удалении от стен­ки снова равна нулю (рис.13.5). Вначале толщина нагретого слоя мала и течение жидкости имеет струйчатый, ламинарный характер. Но по направлению движения толщина слоя увеличивается, и при определенном ее значении течение жидкости становится неустойчивым, волновым, локонообразным и затем перехо­дит в неупорядоченно-вихревое, турбулентное, с отрывом вихрей от стенки. С изменением харак­тера движения изменяется и теплоотдача. При ла­минарном движении вследствие увеличения толщины пограничного слоя коэффициент теплоотдачи по направлению движения убывает, а при турбулентном он резко возрастает и затем по высоте остается постоянным (рис.13.6)

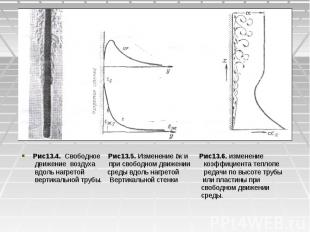
Рис13.4. Свободное Рис13.5. Изменение tж и Рис13.6. изменение Рис13.4. Свободное Рис13.5. Изменение tж и Рис13.6. изменение движение воздуха при свободном движении коэффициента теплопе вдоль нагретой среды вдоль нагретой редачи по высоте трубы вертикальной трубы. Вертикальной стенки или пластины при свободном движении среды.

В развитии свободного движения форма тела играет второсте­пенную роль. Здесь большее значение имеют протяженность поверх­ности, вдоль которой происходит движение, и ее положение. Опи­санная выше картина движения жидкости вдоль вертикальной стенки (или вдоль вертикальной трубы) типична также и для гори­зонтальных труб и тел опальной формы. Характер движения воздуха около нагретых горизонтальных труб различного диаметра представлен на (рис13.7). В развитии свободного движения форма тела играет второсте­пенную роль. Здесь большее значение имеют протяженность поверх­ности, вдоль которой происходит движение, и ее положение. Опи­санная выше картина движения жидкости вдоль вертикальной стенки (или вдоль вертикальной трубы) типична также и для гори­зонтальных труб и тел опальной формы. Характер движения воздуха около нагретых горизонтальных труб различного диаметра представлен на (рис13.7). Около нагретых горизонтальных плоских стенок или плит движение жидкости имеет иной характер и в сильной мере зависит от положения плиты и ее размеров. Если нагретая поверхность обра­щена кверху, то движение протекает по схеме (pис13.8), а. При том

а) а) Рис.13.8. Характер свободного движения жидкости около нагретых горизонтальных плит. Рис. 13.7. Характер свободного движения воздуха около горизонтальных труб. а — d= 28 мм; б - d= 250 мм: вид с торца. Если плита имеет большие размеры, то вследствие наличия с краев сплошного потока нагретой жидкости центральная часть плиты ока­зывается изолированной. Ее вентиляция происходит лишь за счет притока (провала) холодной жидкости сверху (рис13.8,б). Если же нагретая поверхность обращена вниз, то в этом случае движе­ние происходит лишь в тонком слое под поверхностью (рис13.8,в); остальная же масса жидкости ниже этого слоя остается непод­вижной. По изучению интенсивности теплообмена в условиях свобод­ного движения были проведены исследования с разными телами и различными жидкостями. В результате обобщения опытных дан­ных получены критериальные зависимости для средних значений коэффициента теплоотдачи. В этих формулах в качестве опреде­ляющей температуры принята температура окружающей среды tж.

В качестве определяющего размера для горизонтальных труб при­нят диаметр d, а для вертикальных поверхностей — высота h В качестве определяющего размера для горизонтальных труб при­нят диаметр d, а для вертикальных поверхностей — высота h Закономерность средней теплоотдачи для горизонтальных труб диаметром d при 103<GrdжPrж< 108 имеет вид: (13.9) а закономерность средней теплоотдачи для вертикальных поверхно­стей (трубы, пластины) следующая: а) при 103<GrhжPrж<109 (ламинарный режим) Nuhж= 0,76(GrhжPrж)0,25(Prж/Prc)0.25 (13.10) Для газов Pr=const, а Рrж/Ргс=1, и потому все приведенные выше расчетные формулы упрощаются.

13.3.2. Теплоотдача с ограниченном пространстве. 13.3.2. Теплоотдача с ограниченном пространстве. Выше были рас­смотрены условия теплообмена в неограниченном пространстве, где протекало лишь одно явление, например нагрев жидкости, Б ограниченном пространстве явления нагревания и охлаждения жидкости протекают вблизи друг от друга, и разделить их невоз­можно; в этом случае весь процесс надо рассматривать в целом. Вследствие ограниченности пространства и наличия восходящих и нисходящих потоков здесь сильно усложняются условия движения. Они зависят как от формы а геометрических размеров, так и от рода жидкости и интенсивности теплообмена. В вертикальных каналах и щелях в зависимости от их толщины циркуляция жидкости может протекать двояко. Если достаточно велика, то восходящий и нисходящий потоки протекают без взаимных помех (pис13.8, а) и имеют такой же характер, как и вдоль вертикальной поверхности б неограниченном пространстве. Если же мала, то вследствие взаимных помех внутри возникают цир­куляционные контуры (рис.13.8.б).

В горизонтальных щелях процесс определяется взаимным рас­положением нагретых и холодных поверхностей и расстоянием меж­ду ними. Если нагретая поверхность расположена сверху, то цир­куляция совсем отсутствует (рис13.8.в). В горизонтальных щелях процесс определяется взаимным рас­положением нагретых и холодных поверхностей и расстоянием меж­ду ними. Если нагретая поверхность расположена сверху, то цир­куляция совсем отсутствует (рис13.8.в). Если же нагретая по­верхность расположена снизу, то имеются и восходящие и нисходящие потоки которые между собой чередуются (рис13.8. г) В шаровых и горизонтальных цилиндрических прослойках в зависимости от их толщины ( или соотношения диаметров)циркуляция жидкости протекает по схемам (Рис.13.8.д и е). Необходимо обратить внимание, что здесь циркуляция развивается лишь в зоне, лежащей ниже кромки нагретой поверхности. Ниже этой кромки жидкость остается в покое. Если же нагрета внешняя цилиндрическая поверхность, то циркуляция жидкости протекает по схеме (рис.3.30,ж) и охватывает все пространство, расположенное ниже верхней кромки холодной поверхности.

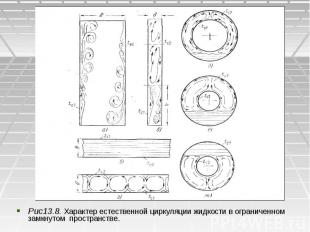
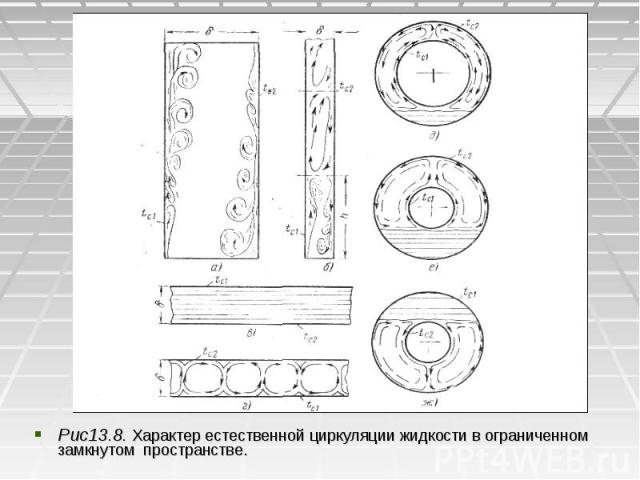
Рис13.8. Характер естественной циркуляции жидкости в ограниченном замкнутом пространстве. Рис13.8. Характер естественной циркуляции жидкости в ограниченном замкнутом пространстве.

Для облегчения расчета, такой сложный процесс конвективного теплообмена принято рассматривать как элементарное явление теплопроводности , вводя при этом понятие, эквивалентного коэффициента теплопроводности Для облегчения расчета, такой сложный процесс конвективного теплообмена принято рассматривать как элементарное явление теплопроводности , вводя при этом понятие, эквивалентного коэффициента теплопроводности Если значение последнего разделить на среды, то получим безразмерную величину которая характеризует собой влияние конвекции и называется коэффициентом конвекции. Так как циркуляция жидкости обусловлена разностью плотностей нагретых и холодных частиц и определяется критерием Gr Pr, то и Ek должно быть функцией того же аргумента т.е. При вычислении критериев подобия не зависимо от формы прослойки за определяющий размер принята ее толщина , а за определяющую температуру – средняя температура жидкости При массовых значениях аргумента Grж Prж<1000 значение функции Ek=1;(lgEk=0). Это значит что при малых значениях Grж Prж теплопередача от горячей стенки к холодной в прослойках обуславливается толко теплопроводностью жидкости. При значении 103< Grж Prж<106 Ek=0.105(Grж Prж)0.3. 13.11 И при 106< Grж Prж<1010 Ek=0.40(Grж Prж)0.2. 13.12

Снижение интенсивности теплопередачи при больших значениях аргумента следует объяснить помехой в движении поднимающихся (нагретых) и опускающихся (охлажденных) струек жидкости (см. рис 13.8 а) В приближенных расчетах вместо (13.11) и (13ю12) для всей области значений аргументов Grж Prж>103. можно принять зависимость Ek=0.18(Grж Prж)0.25. 13.13 Которую можно привести к виду: Ek= 13 где A= .

13.3.3. Теплопередача при поперечном обтекании труб. 13.3.3. Теплопередача при поперечном обтекании труб. Для многих теплообменников, как? например водотрубных котлов, воздухоподогревателей, экономайзеров и др., характерно поперечное расположение труб в потоке теплоносителя. При этом, как указывалось выше, поток жидкости отрывается от омываемой поверхности, движение теплоносителя приобретает очень сложный характер - образуются застойные области, возникают обратные течения; крупные вихри и другие явления, которые искажают естест­венные условия течения, соответствующие форме русла потока Рассмотрим вначале поперечное обтекание одиночной трубы. Из рис13.9, а. где показано поперечное обтекание цилиндра потоком жидкости, видно, что около «экватора» (точнее, при = 820 , где -угол, отсчитываемый от лобовой точки трубы) происходит отрыв струя от поверхности и только около 45% поверхности трубы омы­вается потоком жидкости, кото­рый не отрывается от нее, а ос­тальная часть трубы находится в вихревой зоне, где течение сложное, циркуляционное. В соответствии с таким специфическим характером движения жидкости процесс теплоотдачи по окружности цилиндра имеет своеобразный характер, что видно из рис13.9. 6. где по оси ординат отложено отношение локального значения величины аф к ее среднему по контуру значению.

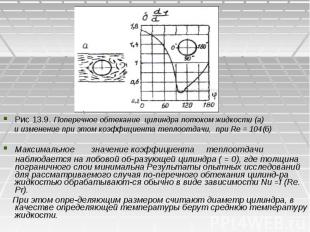
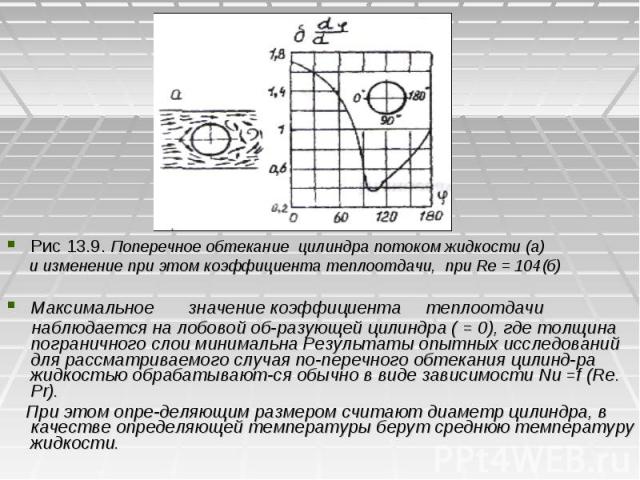
Рис 13.9. Поперечное обтекание цилиндра потоком жидкости (а) Рис 13.9. Поперечное обтекание цилиндра потоком жидкости (а) и изменение при этом коэффициента теплоотдачи, при Re = 104(б) Максимальное значение коэффициента теплоотдачи наблюдается на лобовой об­разующей цилиндра ( = 0), где толщина пограничного слои минимальна Результаты опытных исследований для рассматриваемого случая по­перечного обтекания цилинд­ра жидкостью обрабатывают­ся обычно в виде зависимости Nu =f (Re. Рr). При этом опре­деляющим размером считают диаметр цилиндра, в качестве определяющей температуры берут среднюю температуру жидкости.

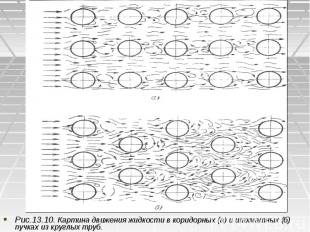
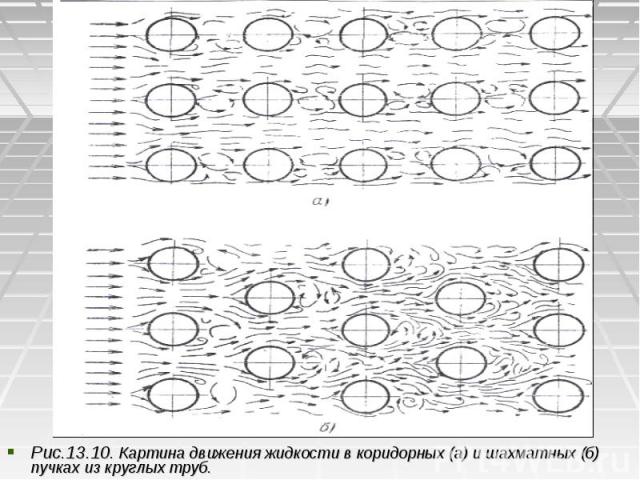
Рис.13.10. Картина движения жидкости в коридорных (а) и шахматных (б) пучках из круглых труб. Рис.13.10. Картина движения жидкости в коридорных (а) и шахматных (б) пучках из круглых труб.

При указанных условиях расчетные формулы для любых жидкостей при угле атаки имеют вид: При указанных условиях расчетные формулы для любых жидкостей при угле атаки имеют вид: Re = 5-103; Nu = 0,5Re0.5Pr0.38(Pr/Prст)0,25 (13.15) Re = 103-105; Nu = 0,25Re0,6Pr0,38(Pr/Prст)0,25 (13.16) Расчет конвективного теплообмена в пучках (пакетах) труб при их поперечном вынужденном обтекании жидкостью представляет собой более сложную задачу. На практике чаще всего встречаются два типа пакетов труб - с коридорным и шахматным расположением. На рисунках (13.10) а. б представлены пучки с коридорным и шахматным расположением труб и показан характер поперечного движения жидкости в пространстве между трубами. На рисунке видно, что в шахматных пучках условия омывания труб во всех ря­дах близки к условиям омывания одиночного цилиндра.

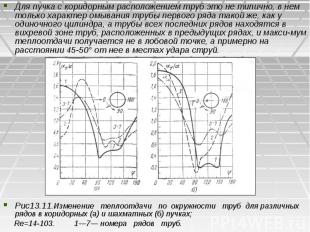
Для пучка с коридорным расположением тpуб это не типично, в нем только характер омывания трубы первого ряда такой же, как у одиночного цилиндра, а трубы всех последних рядов находятся в вихревой зоне труб, расположенных в предыдущих рядах, и макси­мум теплоотдачи получается не в лобовой точке, а примерно на расстоянии 45-50° от нее в местах удара струй. Для пучка с коридорным расположением тpуб это не типично, в нем только характер омывания трубы первого ряда такой же, как у одиночного цилиндра, а трубы всех последних рядов находятся в вихревой зоне труб, расположенных в предыдущих рядах, и макси­мум теплоотдачи получается не в лобовой точке, а примерно на расстоянии 45-50° от нее в местах удара струй. Рис13.11.Изменение теплоотдачи по окружности труб для различных рядов в коридорных (а) и шахматных (б) пучках; Re=14-103. 1—7— номера рядов труб.

На основании обобщения многочисленных опытных данных используют следующие расчетные формулы средней теплоотдачи На основании обобщения многочисленных опытных данных используют следующие расчетные формулы средней теплоотдачи для третьего и последующих рядов труб в пучке для Re = 103-105: при коридорном расположении Nu = O,26Re0,65PrO,33(Pr/Prст)0,25; (13.17) при шахматном расположении Nu= 0,41 Re0.6Pr0.33(Pr/Prст)0,25 . (13.18) В качестве определяющего размера в этих формулах принят внешний диаметр труб пучка, определяющий температуры - средняя температура жидкости Чтобы определить труб первого ряда пучка, нужно найден­ное значение коэффициента теплоотдачи для третьего ряда умно­жить на поправочный коэффициент = 0,6. для труб второго ряда при коридорном пучке - на = 0,9, а при шахматном - на = 0,7. Средний коэффициент теплоотдачи пучка труб в целом опре­деляют путем усреднения вычисленных значений по рядам труб, пользуясь равенством: (13.19) где , , … - коэффициенты теплоотдачи рядов пучка; F1,F2, .., Fn - поверхности нагрева всех труб в ряду. Если F1= F2=F3...= Fn, то = [ + + (п – 2)]/ п.