Презентация на тему: Физические основы механики

Лекция 2 Тема: Физические основы механики Математическая справка: §3. Элементы математического анализа. 2. Элементы кинематики §1. Пространство, время, системы отсчета. §2. Кинематика материальной точки. Содержание лекции: Сегодня: * 900igr.net

Векторное произведение Векторным произведением вектора на вектор назовем вектор , модуль которого а) вектор ортогонален векторам и ; б) из конца вектора кратчайший поворот от вектора (первого сомножителя) к вектору (второму сомножителю) виден против часовой стрелки. (Начала векторов предполагаются совмещенными).         

§3. Элементы математического анализа Производная. Если f(x) - непрерывная функция одной переменной, то ее производной называется Пример: Частная производная. f(x, y, z) - непрерывная функция нескольких переменных. Частной производной по одной из переменных называется: Полная производная сложной функции f(x, y, z, t), где x = x(t), y = y(t), z = z(t), t – параметр (время).

Таблица производных Функция Производная 0

Правила дифференцирования

Неопределенный интеграл

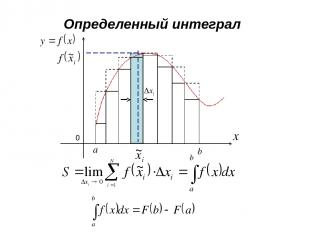
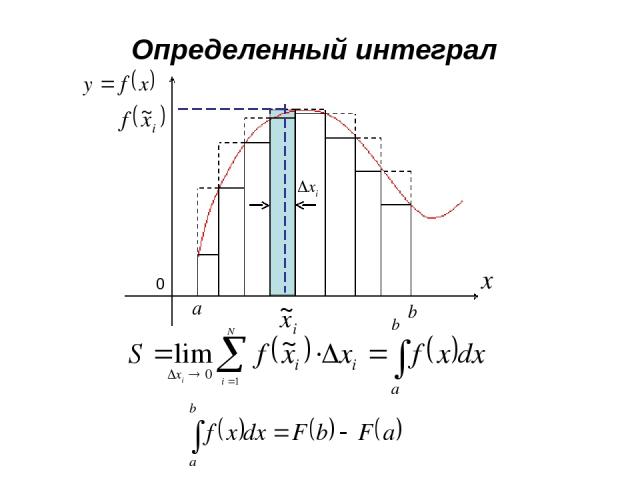
Определенный интеграл 0

2. Элементы кинематики §1. Пространство, время. Системы отсчета

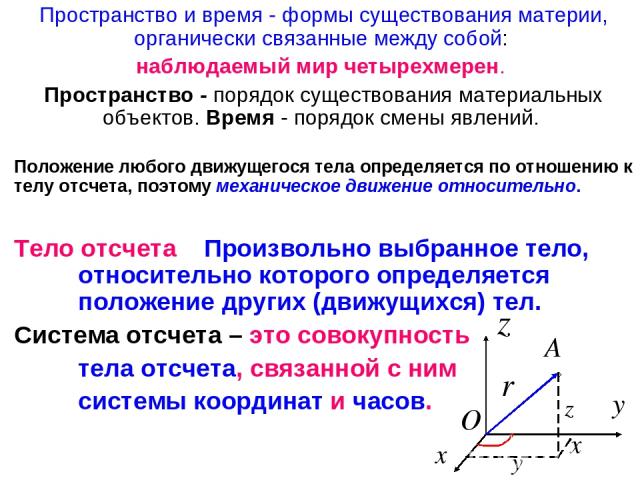
Пространство и время - формы существования материи, органически связанные между собой: наблюдаемый мир четырехмерен. Пространство - порядок существования материальных объектов. Время - порядок смены явлений. Положение любого движущегося тела определяется по отношению к телу отсчета, поэтому механическое движение относительно. Тело отсчета Произвольно выбранное тело, относительно которого определяется положение других (движущихся) тел. Система отсчета – это совокупность тела отсчета, связанной с ним системы координат и часов.

где i, j, k – единичные векторы (орты). Число независимых координат, однозначно определяющих положение тела (или системы тел) в пространстве, называется числом степеней свободы тела (или системы тел). Любые k величин q1, q2, …, qk, однозначно определяющие положение системы, называются обобщенными координатами.

Свободная материальная точка: число степеней свободы k = 3; N-точек: k = 3N. Точка не свободна, а движется по поверхности сферы радиуса R с центром в начале координат Три координаты x, y, z связаны между собой соотношением т.е. k = 3 – n = 3 – 1 = 2, где n – число связей. Обобщенные координаты: q1= x, q2= y или q1= , q2= . Точка движется по заданной кривой например, точка движется по окружности R в плоскости oxy, (две связи n=2): - уравнение сферы и z = 0 – уравнение плоскости k = 3 – n = 3 – 2 = 1. Обобщенные координаты q = x или q = . В общем случае число степеней свободы тела или системы тел, и, следовательно, обобщенных координат k = 3N - n, где N – число материальных точек входящих в состав тела.

«Жесткий» треугольник А(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3): k = 3N - n = 6, где n =3 – число связей на координаты. Уравнения связей: Моделирует абсолютно твердое тело, у которого тоже будет 6 степеней свободы. Из них 3 описывают поступательное движение, 3 – вращательное. Для определения положения необходимо задать: x, y, z; 2) , ; . Если тело закреплено в точке (еще три дополнительные связи), то тело может лишь вращаться вокруг этой точки, остается только три степени свободы. У твердого тела, которое может вращаться вокруг закрепленной оси, остается одна степень свободы, характеризуемая одной обобщенной координатой – углом поворота вокруг этой оси.

§2. Кинематика материальной точки

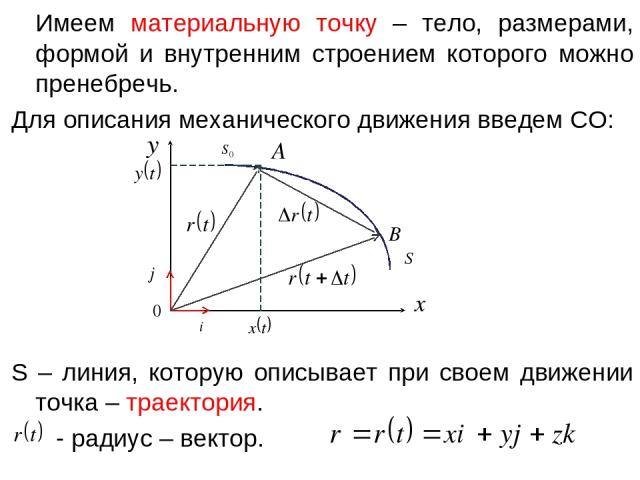
Имеем материальную точку – тело, размерами, формой и внутренним строением которого можно пренебречь. Для описания механического движения введем СО: S – линия, которую описывает при своем движении точка – траектория. - радиус – вектор.

Кинематические уравнения движения - это уравнения, с помощью которых описываются изменения положения материальной точки в пространстве и времени Вектор перемещения - Вектор, соединяющий начальную (1) движения с конечной (2). Путь S - расстояние, пройденное точкой вдоль траектории движения от начальной точки (1) до конечной (2), величина скалярная. При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения равен пройденному пути:

Рассмотрим еще раз рисунок. Возьмем отношение - вектор средней скорости перемещения между точками А и В. Фиксируем положение А, положение В выбираем ближе к точке А и найдем новое отношение Повторяем эту процедуру, выбираем точку В ближе и ближе к фиксированной точке А. Предел последовательности указанного отношения дает мгновенную скорость материальной точки в положении А.

Из способа нахождения мгновенной скорости ясно, что она всегда направлена по касательной к траектории. Вектор мгновенной скорости определяет быстроту изменения радиус-вектора r со временем, т.е. быстроту изменения положения точки в пространстве.

Аналогично определяется и вектор мгновенного ускорения. Выберем два последовательных положения материальной точки А и В. Найдем мгновенную скорость в этих положениях и . 1) Перенесем вектор параллельно самому себе из В в А. 2) Найдем разность векторов и . Отношение представляет собой вектор среднего ускорения между точками А и В. 3) Будем повторять процедуру, постоянно приближаясь к фиксированной точке А. Предел последовательности таких отношений (предел средних ускорений) – мгновенное ускорение материальной точки в положении А: A В

Ускорение и его составляющие Ускорение – Характеристика неравномерного движения, определяющая быстроту изменения скорости по модулю и направлению. Среднее ускорение – векторная величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло. Мгновенное ускорение – векторная величина, определяемая первой производной скорости по времени

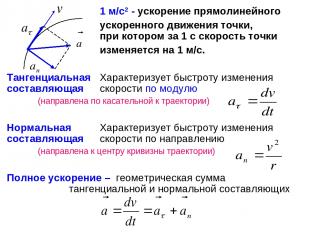
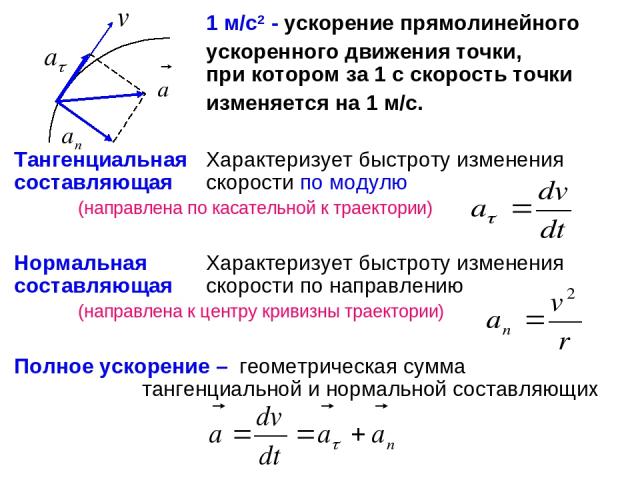
1 м/с2 - ускорение прямолинейного ускоренного движения точки, при котором за 1 с скорость точки изменяется на 1 м/с. Тангенциальная Характеризует быстроту изменения составляющая скорости по модулю (направлена по касательной к траектории) Нормальная Характеризует быстроту изменения составляющая скорости по направлению (направлена к центру кривизны траектории) Полное ускорение – геометрическая сумма тангенциальной и нормальной составляющих

Задача 1. Уравнение движения материальной точки вдоль оси OX имеет вид x = A + Bt + Ct3, где А = 2 м, В = 1,5 м/с, С = -0,5 м/с3. Найти: Координату x, скорость vx, ускорение аx точки в момент времени t = 2 c. Среднюю скорость и среднее ускорение за этот промежуток времени. Решение:

Средняя скорость – отношение всего пути, пройденного телом ко времени. Найдем значение времени, когда тело изменило направление движения на противоположное. В этот момент времени мгновенная скорость равна 0. Определим путь за время 2 с:

Среднее ускорение – - скорость в момент времени t2 = 2 c. - скорость в момент времени t1 = 0 c.

Задача 2. Электрон движется в некоторой системе отсчета из начального положения, определяемого радиус-вектором , где x0 = 3 м, z0 = 1 м с начальной скоростью , где v0y = 2 м/с и ускорением , где А = 12 м/с2, В = 8 м/с2. Найти: Координату z электрона в момент времени t = 0,5 с. 2. Скорость электрона в момент времени t = 1 с, 3. Угол между радиусом–вектором и вектором скорости в момент времени t = 0 с.

Решение: 2) Модуль скорости, если ускорение зависит от времени определяется: Модуль ускорения: Кинематические уравнения скоростей:

Учитываем начальные условия м/с: Вектор модуля скорости: (м/с) Модуль скорости в момент времени t = 1 с: м/с; 1) Координата z электрона в момент времени t = 0,5 с:

3) Угол между радиусом–вектором и вектором скорости в момент t = 0 с определим, используя скалярное произведение этих векторов: Следовательно,

Задача 3. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны . Уравнение движения автомобиля , где А = 10 м, В = 10 м/с, С = -0,5 м/с2. Найти: Скорость автомобиля v, его тангенциальное ускорение at, нормальное an и полное ускорения a в момент времени t = 5 с. 2. Длину пути и модуль перемещения автомобиля за интервал времени t = 10 с, отсчитанный с момента начала движения.

Решение: 1) Мгновенная скорость – первая производная от координаты по времени: Тангенциальное ускорение найдем, взяв первую производную от скорости по времени: Нормальное ускорение: Полное ускорение

2) Путь, пройденный автомобилем в одном направлении, равен изменению координаты: Модуль перемещения:

1. Средняя скорость Задача 1. Первую четверть пути автомобиль двигался со скорость 60 км/ч, остальной путь – со скоростью 20 км/ч. Найдите среднюю скорость автомобиля. Решение: Средняя скорость Полное время движения равно сумме времен движения на отдельных участках: Подставляем: Получим:

2. Бросок под углом Задача 2.Из окна, находящегося на высоте h0 = 7,5 м, бросают камень под углом 450 к горизонту. Камень упал на расстоянии s = 15 м от стены дома. С какой скоростью v0 был брошен камень? Решение: Запишем зависимость координат камня от времени

Учтем, что в момент падения Из первого уравнения выразим время Подставим во второе уравнение

3. Движение в поле тяжести Задача 3. Камень брошен вертикально вверх со скоростью v0 = 50 м/с. Через сколько секунд его скорость будет равна v = 30 м/с и направлена вниз. Решение: Формулы равноускоренного движения действуют все время равноускоренного движения. Направим ось OY вертикально вверх. Воспользуемся формулой: В данном случае Получаем: Проверка: за время t1 = v0/g = 5 c – поднимается вверх, а затем за t2 = t – t1= 3 с набирает скорость v = g t2= 30 м/с.