Презентация на тему: 2. Работа электрического поля

Работа электростатического поля 10 класс учитель физики, МГОЛ № 1, Сакович А.Л. Могилев, 2014, 2015, 2016 Это материалы сайтов www.alsak.ru и web-physics.ru

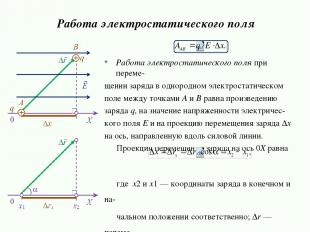
Работа электростатического поля при переме- щении заряда в однородном электростатическом поле между точками А и В равна произведению заряда q, на значение напряженности электричес- кого поля E и на проекцию перемещения заряда Δx на ось, направленную вдоль силовой линии. Проекция перемещения заряда на ось 0Х равна где x2 и x1 — координаты заряда в конечном и на- чальном положении соответственно; Δr — переме- щение заряда; α — угол между направлением пере- мещения и силовой линией. Работа электростатического поля

Поле, работа сил которого не зависит от формы траектории и на замкнутой траектории равна нулю, называется потенциальным или консервативным. Электростатическое поле — это потенциальное поле. Работа электростатического поля

Потенциальная энергия Wp заряда q в электростатическом поле Потенциальная энергия где Е — значение напряженности электрическо- го поля в точке, где находится заряд; х — координата заряда на оси 0Х, направлен- ной вдоль силовой линии. Координата x зависит от выбора системы отсчета (СО), поэтому и потенциальная энергия Wp заряда зависит от выбора СО. Е

Потенциальная энергия Wp взаимодействия двух зарядов равна где Если q1 и q2 — одноименные заряды, то Wp > 0, если q1 и q2 — разные по знаку заряды, то Wp < 0. Потенциальная энергия Рассмотрим два точечных заряда q1 и q2, расположенных на расстоянии r друг от друга. — коэффициент пропорциональности.

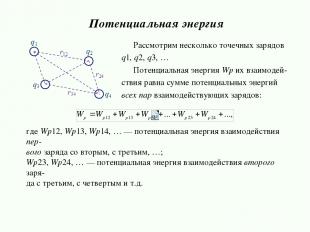
где Wp12, Wp13, Wp14, … — потенциальная энергия взаимодействия пер- вого заряда со вторым, с третьим, …; Wp23, Wp24, … — потенциальная энергия взаимодействия второго заря- да с третьим, с четвертым и т.д. Потенциальная энергия Рассмотрим несколько точечных зарядов q1, q2, q3, … Потенциальная энергия Wp их взаимодей- ствия равна сумме потенциальных энергий всех пар взаимодействующих зарядов:

Потенциальная энергия Wp зарядa q в точке А: Найдем значение величины Характеристика поля В точку А однородного электростатического поля с напряженностью E помещаем заряд q. Выберем СО, в которой координата точки А равна x1. Введем еще одну характеристику электрического поля.

Потенциальная энергия Wp зарядa 2q в точке А: Найдем значение величины Характеристика поля В точку А однородного электростатического поля с напряженностью E помещаем заряд 2q.

Аналогичный результат мы получим, если будем помещать в точку А другие заряды. Следовательно, величина не зависит от величины заряда, который мы помещаем в электри- ческое поле; но зависит от параметров электрического поля: от E (напряженности поля), от x (координаты точки поля). Характеристика поля

Потенциал Новая характеристика электрического поля — потенциал φ поля в данной точке. Потенциал электростатического поля φ в данной точке простран- ства — это скалярная физическая величина, равная циальной энергии Wp, которой обладает точечный заряд q в данной точ- ке пространства, к величине этого заряда. Единицей измерения потенциала является вольт (В). Потенциал — это энергетическая характеристика электрического поля. отношению потен-

Пусть электрическое поле создано точечным зарядом q. В точке А, расположенной на расстоянии r от заряда q, потенциал поля Потенциал где — коэффициент пропорциональности.

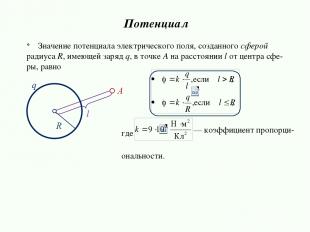
где ональности. Значение потенциала электрического поля, созданного сферой радиуса R, имеющей заряд q, в точке A на расстоянии l от центра сфе- ры, равно Потенциал — коэффициент пропорци-

Потенциал (как и потенциальная энергия заряда) зависит от выбо- ра СО (нулевого уровня). За нулевой потенциал в технике выбирают: потенциал поверхности Земли или потенциал проводника, соединенного с землей (заземленный). Свойства Потенциала φ = 0

За нулевой уровень потенциала в физике принимается бесконечно удаленная от зарядов, создающих поле. Если электрическое поле создано: зарядом q > 0, то потенциал этого поля зарядом q < 0, то φ < 0. Свойства Потенциала любая точка, φ > 0;

Потенциал поля, созданного несколькими зарядами, в некоторой точке пространства равен емых в этой точке каждым зарядом в отдельности. Свойства Потенциала Пусть электрическое поле создано зарядами q1, q2, q3. Тогда 3. Принцип суперпозиции. алгебраической сумме потенциалов, создава-

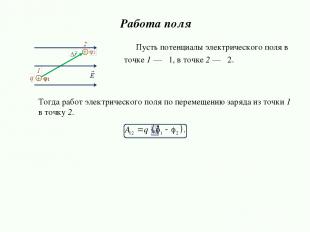
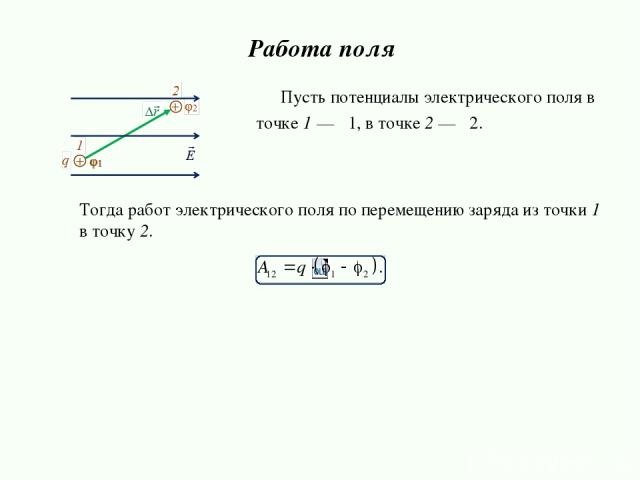
Тогда работ электрического поля по перемещению заряда из точки 1 в точку 2. Работа поля Пусть потенциалы электрического поля в точке 1 — φ1, в точке 2 — φ2.

Разность потенциалов между данными точками электростатическо- го поля — это скалярная физическая величина, численно равная сил поля по перемещению заряда в 1 Кл между этими точками. Разность потенциалов обозначается Не путайте изменение потенциала и разность потенциала Разность потенциалов (φ1 – φ2) не зависит от выбора СО. Потенциал работе измеряется в вольтах (В).

Разность потенциалов φ1 – φ2 называют электрическим напряжени- ем между точками поля 1 и 2, обозначают U12 или U: Напряжение между данными точками электростатического поля — это скалярная физическая величина, численно равная по перемещению заряда в 1 Кл между этими точками. Измеряется в вольтах (В). Данная формула верна, если на участке поля между двумя точками работа сторонних сил равна нулю. Не путайте напряжение U и напряженность E. напряжение работе сил поля

Не системная единица измерения работы электрического поля — электронвольт (эВ). 1 эВ равен работе, совершаемой силами электрического поля при перемещении электрона (е = 1,6·10-19 Кл) между двумя точками, напря- жение между которыми равно 1 В. 1 эВ = 1,6·10–19 Кл·1 В = 1,6·10–19 Дж. 1 МэВ = 106 эВ = 1,6·10–13 Дж. напряжение

Напряженность и Напряжение где Δx — силовой линии. расстояние между точками 1 и 2 вдоль Из этой формулы получаем новую единицу измерения напряжен- ности: Формула связи между напряженностью E и напряжением U одноро- дного электростатического поля.

Поместим в однородное электростатическое поле с напряженность E положительный заряд q (в точке А). Предположим, что заряд переместился из точки A в точку B. Найдем, чему равна работа электростатичес- кого поля A по перемещению заряда. Вывод формул Из механики: работа силы F равна Чему равна сила F, если известны значения q и E? Куда она направлена? Между чем измеряется угол α?

Направим ось 0Х вдоль силовой линии и пост- роим проекцию перемещения Δrx на ось 0Х. Чему равна проекция Δrx? Таким образом мы имеем: Вывод формул

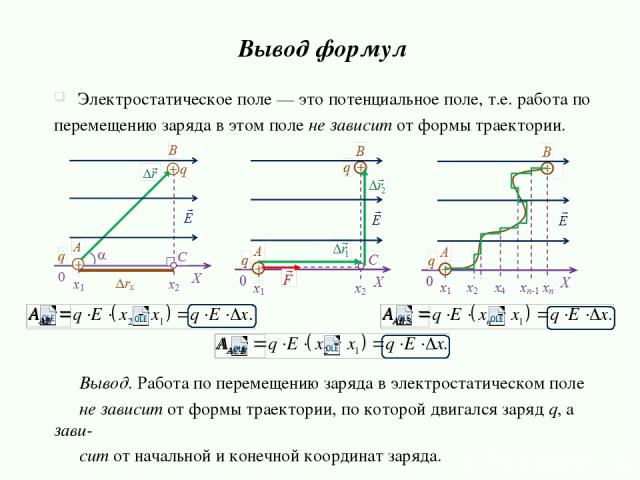
Найдем работу поля при перемещении заряда q по траектории ACB. Вывод формул Электростатическое поле — это потенциальное поле, т.е. работа по перемещению заряда в этом поле не зависит от формы траектории.

Вывод формул Электростатическое поле — это потенциальное поле, т.е. работа по перемещению заряда в этом поле не зависит от формы траектории. Найдем работу поля при перемещении заряда q по криволинейной траектории.

Вывод формул Электростатическое поле — это потенциальное поле, т.е. работа по перемещению заряда в этом поле не зависит от формы траектории. Вывод. Работа по перемещению заряда в электростатическом поле не зависит от формы траектории, по которой двигался заряд q, а зави- сит от начальной и конечной координат заряда.

Найдем работу поля при перемещении заряда q по траектории ABCA. Вывод формул Работа по перемещению заряда в электростатическом поле на замкну- той траектории равна нулю.

Из механики: работа консервативных сил равна изменению потенци- альной энергии, взятому с противоположным знаком: Вывод формул С другой стороны, выше доказали, что

Найдем работу электрического поля по перемещению заряда из точ- ки 1 в точку 2. Вывод формул Пусть потенциалы электрического поля в точке 1 — φ1, в точке 2 — φ2. Тогда потенциальные энергии заряда q в точке 1 и в точке 2 будут равны:

Приравнивая два выражения для работы A12, найдем E: Вывод формул Пусть потенциалы однородного электростатичес- кого поля в точке 1 — φ1, в точке 2 — φ2; координаты этих точек — x1 и x2; напряженность поля — E. Из точки 1 в 2 перемещается заряд q. В этом случае работу электрического поля можно найти двумя способами:

Литература Физика – 10. § 16-17, С. 121-127, 130-132. Подробнее

Здесь может быть ваша реклама