Презентация на тему: Нейтронная звезда

Конференция по физике и астрономии для молодых ученых Санкт-Петербурга и Северо-Запада 28 октября 2010 года Е. Крышень, Б. Л. Бирбраир (ПИЯФ) Сжимаемость ядерной материи и нейтронные звезды 900igr.net
* Содержание Внутреннее строение нейтронных звезд Уравнение состояния ядерной материи и ограничения на массу НЗ Модель релятивистского среднего поля и многочастичные силы Методы определения сжимаемости ядерной материи Рассчитанные массы нейтронных звезд в зависимости от сжимаемости
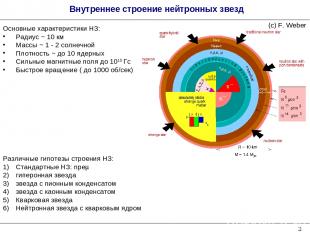
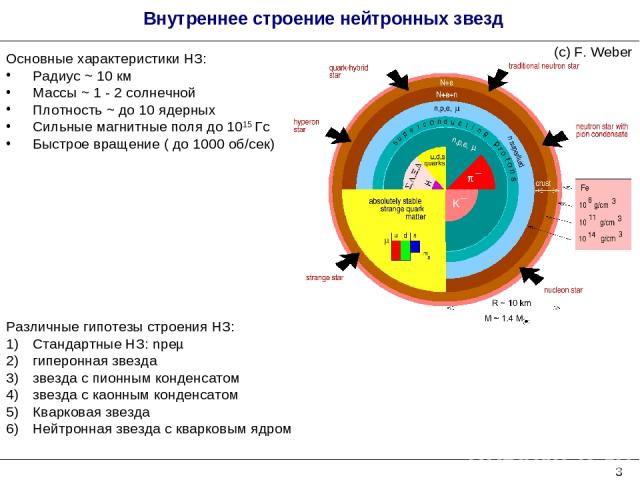
* Внутреннее строение нейтронных звезд Различные гипотезы строения НЗ: Стандартные НЗ: npeµ гиперонная звезда звезда с пионным конденсатом звезда с каонным конденсатом Кварковая звезда Нейтронная звезда с кварковым ядром Основные характеристики НЗ: Радиус ~ 10 км Массы ~ 1 - 2 солнечной Плотность ~ до 10 ядерных Сильные магнитные поля до 1015 Гс Быстрое вращение ( до 1000 об/сек) (с) F. Weber

* Измеренные массы нейтронных звезд
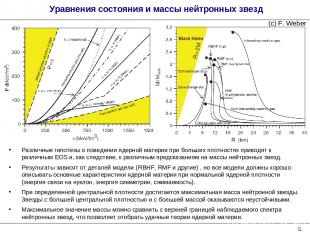
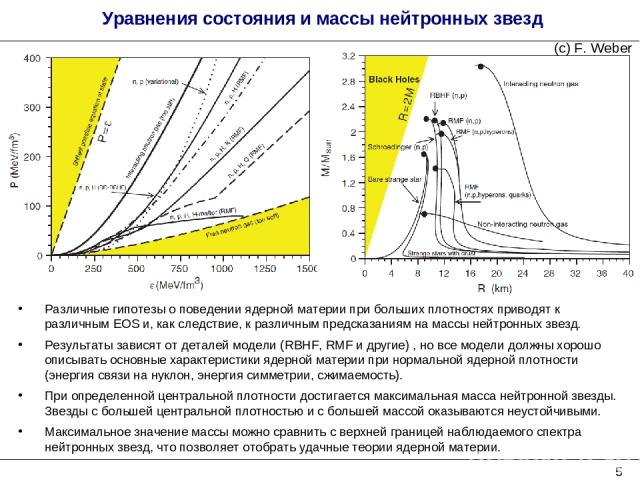
Уравнения состояния и массы нейтронных звезд Различные гипотезы о поведении ядерной материи при больших плотностях приводят к различным EOS и, как следствие, к различным предсказаниям на массы нейтронных звезд. Результаты зависят от деталей модели (RBHF, RMF и другие) , но все модели должны хорошо описывать основные характеристики ядерной материи при нормальной ядерной плотности (энергия связи на нуклон, энергия симметрии, сжимаемость). При определенной центральной плотности достигается максимальная масса нейтронной звезды. Звезды с большей центральной плотностью и с большей массой оказываются неустойчивыми. Максимальное значение массы можно сравнить с верхней границей наблюдаемого спектра нейтронных звезд, что позволяет отобрать удачные теории ядерной материи. (с) F. Weber *

* Модель релятивистского среднего поля (RMF) Основные особенности модели RMF, используемой в данной работе: Используются пустотные константы нуклон-нуклонных взаимодействий, полученные из различных версий Боннского потенциала Гиперонные константы связи определяются по правилам кваркового счета Зависимость от плотности учитывается путем введения нелинейностей и прямым учетом многочастичных сил Рассмотрено влияние странных скалярного и векторного мезонов (f и φ) Основные характеристики ядерной материи, используемые для определения параметров модели: равновесная плотность Энергия связи на нуклон Энергия симметрии Сжимаемость ядерной материи

* Введение многочастичных сил 1. Введение нелинейностей в изоскалярных каналах: 2. Прямое введение многочастичных сил в изовекторных каналах: Определение параметров нелинейностей: λ3 λ4 λω – по равновесной плотности n0, энергии связи B0 и сжимаемости K ξ – по наблюдаемой энергии симметрии S

* Сжимаемость ядерной материи Способы определения сжимаемости: Энергии возбуждения гигантских монопольных резонансов – вызывает сомнения, так как энергии ГМР меньше энергии соответсвующих частично-дырочных переходов в спектре одночастичных состояний. Модель Маерса-Святецкого – Thomas-Fermi фит на измеренные массы ядер, содержит 7 подгоночных параметров. Эксперименты по столкновению тяжелых ионов (изучение выхода странности и эллиптических потоков) – результаты получены при конечных температурах, при допущении пустотных сечений взаимодействия нуклонов. Полученные значения сильно моделезависимы. Общепринятым на сегодняшний день является значение ~ 230 МэВ
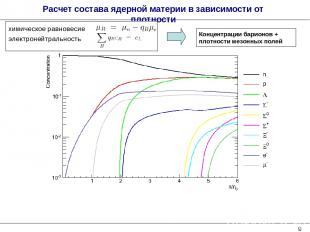
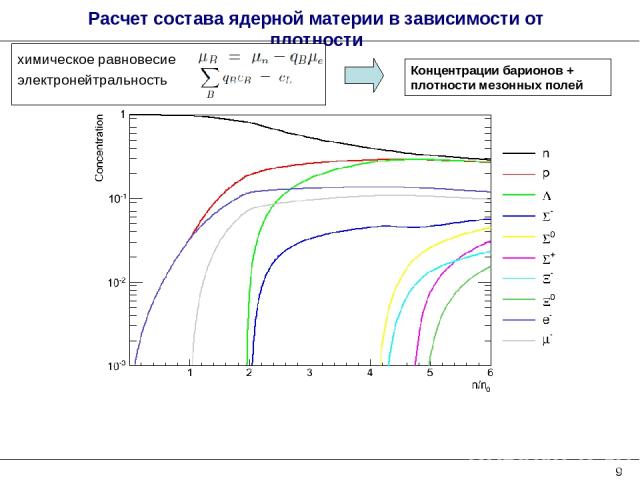
* Расчет состава ядерной материи в зависимости от плотности Концентрации барионов + плотности мезонных полей
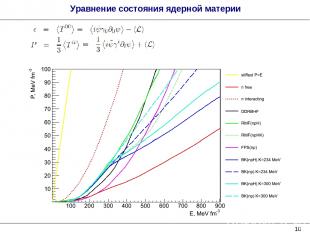
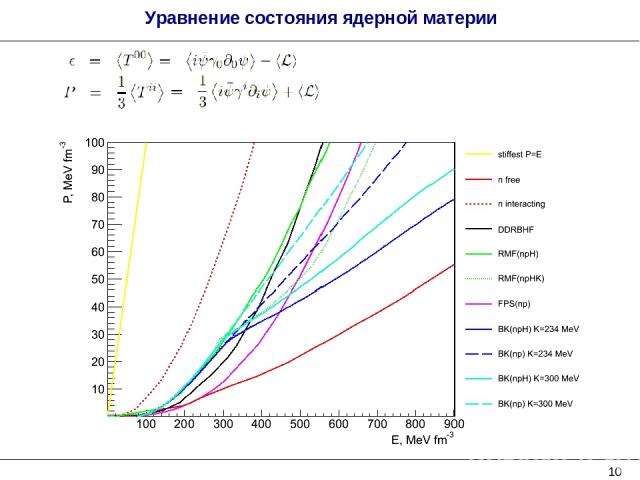
* Уравнение состояния ядерной материи
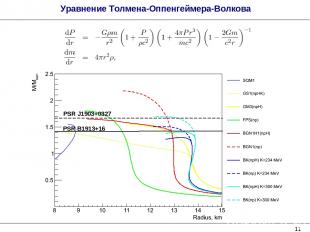
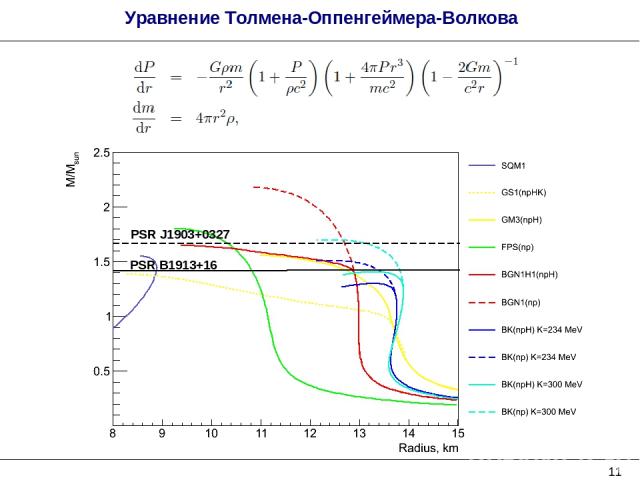
* Уравнение Толмена-Оппенгеймера-Волкова PSR B1913+16 PSR J1903+0327
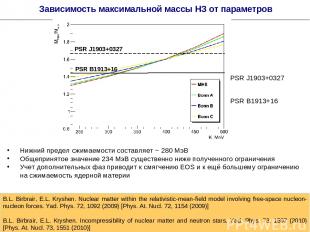
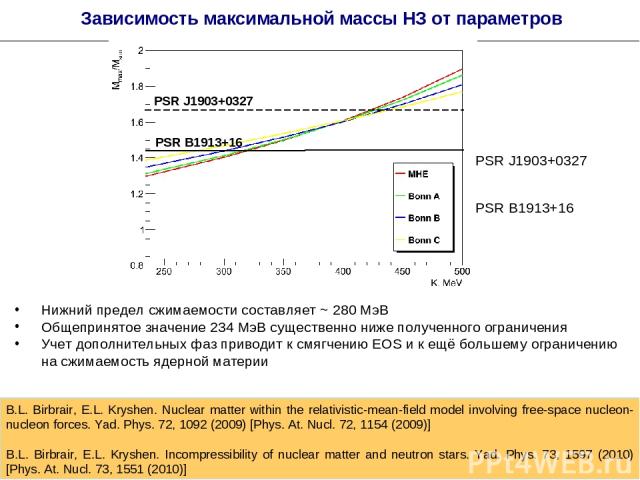
Нижний предел сжимаемости составляет ~ 280 МэВ Общепринятое значение 234 МэВ существенно ниже полученного ограничения Учет дополнительных фаз приводит к смягчению EOS и к ещё большему ограничению на сжимаемость ядерной материи * Зависимость максимальной массы НЗ от параметров PSR J1903+0327 PSR B1913+16 B.L. Birbrair, E.L. Kryshen. Nuclear matter within the relativistic-mean-field model involving free-space nucleon-nucleon forces. Yad. Phys. 72, 1092 (2009) [Phys. At. Nucl. 72, 1154 (2009)] B.L. Birbrair, E.L. Kryshen. Incompressibility of nuclear matter and neutron stars. Yad. Phys. 73, 1597 (2010) [Phys. At. Nucl. 73, 1551 (2010)] PSR B1913+16 PSR J1903+0327