Презентация на тему: Лекция 2. Бинарные отношения и свойства

Бинарным отношением Т(М) на множестве М называется подмножество , Бинарным отношением Т(М) на множестве М называется подмножество , Инфиксная форма записи бинарного отношения a T b =

Обратное отношение Обратное отношение Дополнительное отношение Тождественное отношение Универсальное отношение

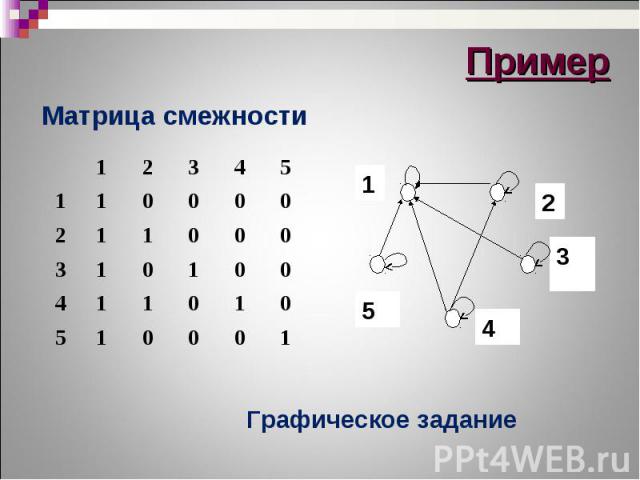
Перечислением, как множество пар Перечислением, как множество пар Графически, когда каждый элемент х множества М представляется вершиной, а пара представляется дугой из х в у Матричным способом, с помощью матрицы смежности или матрицы инцинденций Фактор-множеством

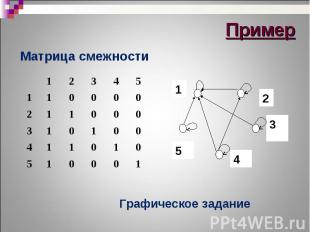
Матрица смежности Матрица смежности

Фактор-множество R/M множества М по отношению к R называется множество окрестностей единичного радиуса для всех элементов М при заданном R Фактор-множество R/M множества М по отношению к R называется множество окрестностей единичного радиуса для всех элементов М при заданном R

называется функцией, если для каждого элемента х найдется не более одного элемента у такого, что , т.е. выполняется свойство однозначности полученного результата называется функцией, если для каждого элемента х найдется не более одного элемента у такого, что , т.е. выполняется свойство однозначности полученного результата Множество X - область определения функции, и множество Y - область значений функции Х и У могут не иметь общих элементов

Функция F: X →Y называется инъективной, или инъекцией, или вложением, если она переводит разные элементы Х в разные У, то есть Функция F: X →Y называется инъективной, или инъекцией, или вложением, если она переводит разные элементы Х в разные У, то есть

Функция F: X → Y называется сюръективной, или сюръекцией, или наложением, если множество ее значений есть все Y, т.е. Функция F: X → Y называется сюръективной, или сюръекцией, или наложением, если множество ее значений есть все Y, т.е.

Функция F: X →Y называется биекцией или взаимно однозначным соответствием, если она одновременно является инъекцией и сюръекцией (вложением и наложением) Функция F: X →Y называется биекцией или взаимно однозначным соответствием, если она одновременно является инъекцией и сюръекцией (вложением и наложением)

Частным случаем функции является операция О Частным случаем функции является операция О В этом случае область значения Х и область определения У совпадают, т.е

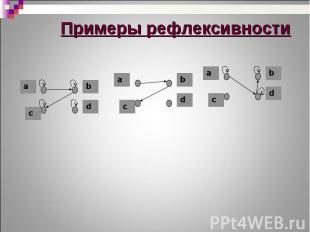
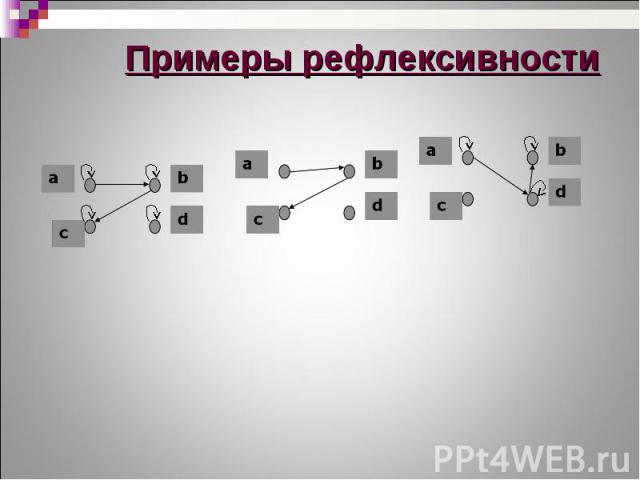
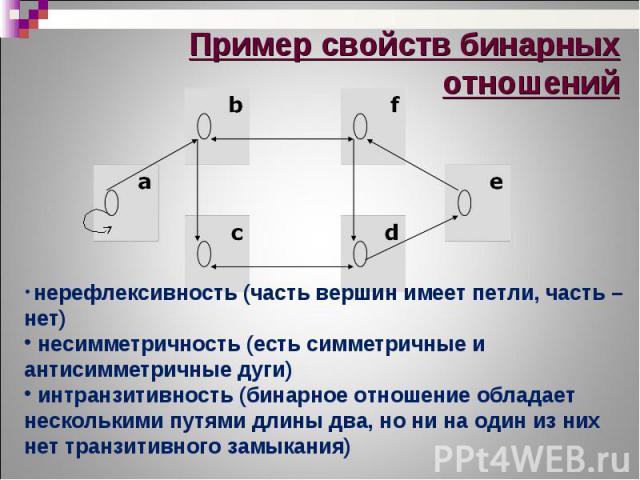
Бинарное отношение T(M) называется рефлексивным тогда и только тогда, когда для каждого элемента пара (х, х) принадлежит этому бинарному отношению, т.е. Бинарное отношение T(M) называется рефлексивным тогда и только тогда, когда для каждого элемента пара (х, х) принадлежит этому бинарному отношению, т.е. Бинарное отношение T(M) называется иррефлексивным тогда и только тогда, когда для каждого элемента пара (х, х) не принадлежит этому бинарному отношению, т.е.

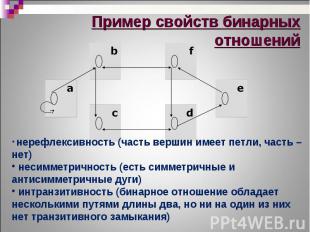
Если бинарное отношение T(M) Если бинарное отношение T(M) не обладает ни свойством рефлексивности, ни свойством иррефлексивности, то оно является нерефлексивным

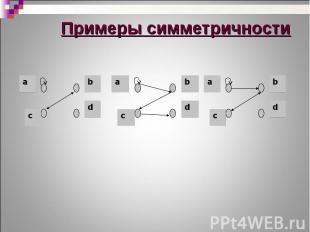
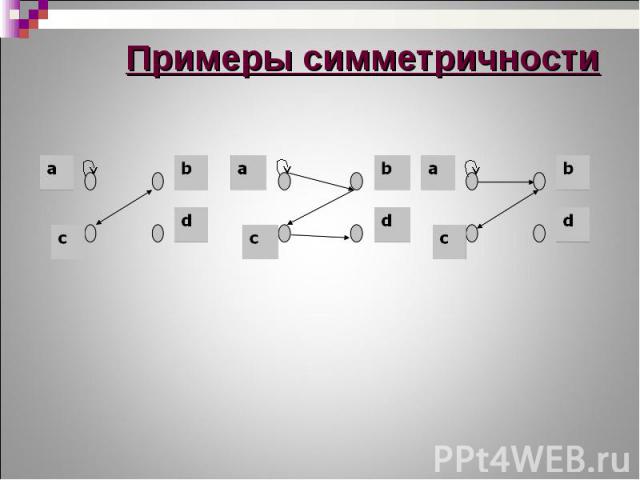
Бинарное отношение T(M) называется симметричным тогда и только тогда, когда для каждой пары (х, у)из Т, обратная пара Бинарное отношение T(M) называется симметричным тогда и только тогда, когда для каждой пары (х, у)из Т, обратная пара (у, х) также принадлежит этому бинарному отношению, т.е. Бинарное отношение T(M) называется антисимметричным тогда и только тогда, когда для каждой пары различных элементов (х, у) из Т пара (у, х) не принадлежит этому бинарному отношению, т.е.

Если бинарное отношение T(M) не обладает ни свойством симметричности, ни свойством антисимметричности, то оно является несимметричным Если бинарное отношение T(M) не обладает ни свойством симметричности, ни свойством антисимметричности, то оно является несимметричным

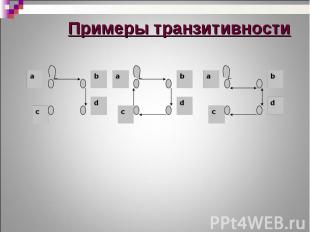
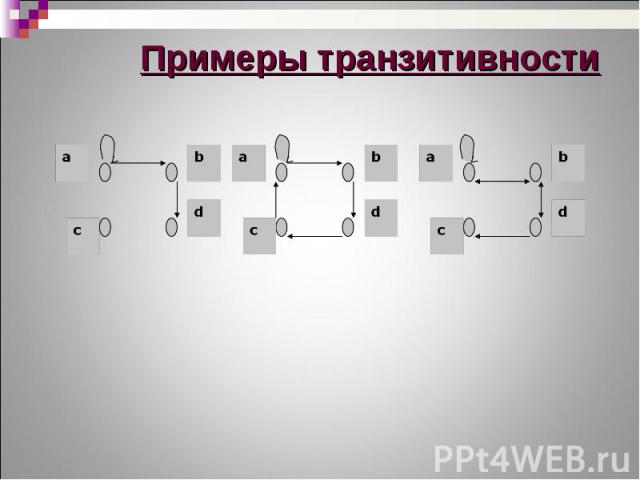
Бинарное отношение T(M) называется транзитивным тогда и только тогда, когда для каждых двух пар элементов (х, у) и (у, z), принадлежащих бинарному отношению, пара (x, z) также принадлежит этому бинарному отношению, т.е. Бинарное отношение T(M) называется транзитивным тогда и только тогда, когда для каждых двух пар элементов (х, у) и (у, z), принадлежащих бинарному отношению, пара (x, z) также принадлежит этому бинарному отношению, т.е.

Если бинарное отношение T(M) не обладает ни свойством транзитивности, ни свойством интранзитивности, то оно является нетранзитивным Если бинарное отношение T(M) не обладает ни свойством транзитивности, ни свойством интранзитивности, то оно является нетранзитивным